taoky 阵列恢复大师
CTF-Writeups-阵列恢复大师
阵列恢复大师
题解作者:taoky
出题人、验题人、文案设计等:见 Hackergame 2021 幕后工作人员。
题目描述
-
题目分类:general
-
题目分值:1 - RAID 0(200)+ 2 - RAID 5(250)
2021 年 10 月 3 日,阴转小雨。
你发现你运行在实验室机器上的炼丹脚本挂了。
「好好的国庆假期,怎么我还得来改程序……」收到邮件通知后,你登录了机器,看到的却是一大堆 Input/Output Error,回过神来才发现,放数据的阵列好像出了问题。
「完了!上面的数据我从来没有备份过!这下赶不上 DDL 发不了 paper 了!」你赶忙跑到机房,检查了一下阵列的情况——看起来盘没坏,都能读,只是可能是受到神秘宇宙射线(误)的影响,阵列的管理页面看不了,每块盘的 RAID 元数据好像也全不见了,更要命的是,你忘了当初组阵列时候盘的顺序和其他的参数。怎么恢复数据呢?上网搜索一下,好像得花不少钱。但你听说你的同学最近在搞信息什么大赛——或许可以让他们试试?
以下是两个压缩包,分别是一个 RAID 0 阵列的磁盘压缩包,和一个 RAID 5 阵列的磁盘压缩包,对应本题的两小问。你需要解析得到正确完整的磁盘阵列,挂载第一个分区后在该分区根目录下使用 Python 3.7 或以上版本执行 getflag.py 脚本以获取 flag。磁盘数据保证无损坏。
RAID 0 阵列压缩包,SHA256: f73bee3a2dce201566573f51bd28026c467182601eb6e55130db10c7c0c8127f
RAID 5 阵列压缩包,SHA256: 5eb1d2042ab5f8e2ee1508bf5e66632b4c307a595099e499aa9bc2a7255a6009
背景
这道题的背景是,USTCLUG 在今年 3 月份惨遭阵列问题(阵列是 RAID 10),结果整个三月份我们都在想办法恢复。要去找阵列恢复服务真的挺贵的……不过因为大部分「坏盘」实际都能读取,我们把能组成 RAID 0 的盘全盘 ddresuce 下来,然后根据 SAN 管理页面猜顺序,由 @zzh1996 写程序验证之后搞了个 FUSE 脚本,这样才在没有破费(不含新硬盘成本和人力成本)的情况下把数据都救回来(虚拟机有备份,但是 LUGFTP 没有设置备份……这是我们的问题,现在已经整上备份了)。
注意:数据无价,以上操作请勿贸然模仿!
在验证的时候,我们发现数据是「有规律」的:可视化之后可以拼图来判断出正确的参数。这也是这道题的重要思路。如果在 CTF 里这道题的分类应该是 forensics(取证)。
这道题的一个遗憾是:我错误估计了 RAID 0 和 RAID 5 的实际难度,导致分值更高的 RAID 5 做出来的人更多。
概论
RAID (Redundant Array of Independent Disks) 的概念操作系统课上肯定都会讲,如果没有上过课也可以直接在网上搜索了解。简单地说,把多块盘放在一起,可以以 RAID 的方式组成一块盘,并且根据 RAID 等级的不同,最后得到的磁盘的大小、性能、容错性会有不同。
RAID 有一些重要的参数:
- RAID 等级。这里是 RAID 0 或者 RAID 5;
- 块大小 (Block size / Chunk size)。常见的块大小一般是 2 的次幂,从 32 KB 到 1024 KB 不等(更多/更少也可以);
- 磁盘顺序/映射。
虽然 RAID 5 似乎「更简单」,我还是想从 RAID 0 小题开始写。到最后大家会发现,这道题和拼图本质上差不多(
RAID 0
RAID 0 无容错(一块盘坏了就全完了)。以 4 块盘的 RAID 0 为例子,数据存储大致长成下面这样:
| 盘 1 | 盘 2 | 盘 3 | 盘 4 |
|---|---|---|---|
| 0 | 1 | 2 | 3 |
| 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 |
其中每个标号都代表了一个块,可以看到 RAID 0 的结构还是很简单的。另一个显然的结论是,在顺序读取大文件的时候,RAID 0 的读取带宽是所有盘的和,提升了阵列的性能。
本题给了 8 个磁盘文件。首先 file 一下看看:
$ file *.img
1GHGGrmaMM0.img: data
5qiSQnlrA4Y.img: data
d3Be7V0EVKo.img: data
eRL2MQSdOjo.img: data
ID7sM2RWkyI.img: data
jCC60mutgoE.img: data
RApjvIxRlu0.img: data
wlOUASom2fI.img: DOS/MBR boot sector; partition 1 : ID=0xee, start-CHS (0x0,0,2), end-CHS (0x3ff,255,63), startsector 1, 262143 sectors, extended partition table (last)
可以看到 wlOUASom2fI.img 有 MBR 头,并且第一块分区 ID 是 0xee。这表明整块磁盘实际上是 GPT 格式的,并且 wlOUASom2fI.img 是第一块盘。
接下来分析 GPT 的元信息(建议先找一份 GPT 结构的介绍)。使用你最喜欢的十六进制编辑器打开 wlOUASom2fI.img。(对 macOS 用户,个人推荐使用 Hex Fiend;用 hexdump 也是可以的!)
首先,GPT 的 signature (magic number) “EFI PART” 在 0x200 = 512 的位置,代表一个 LBA (Logical Block Address) 的大小是 512 B。题目已经说了 flag 在第一个分区,所以直接来看 LBA 2 的内容(第一个分区表项,在 0x400 的位置)。
在 0x400 + 0x20 的位置是第一个分区的初始 LBA,得到十六进制 00080000 00000000,转换为小端序 64 位整数是 2048,代表第一个分区在 2048 * 512 = 1048576 B = 1 MB (0x100000) 的位置。
那么它在哪里呢?为了解决这个问题,这里介绍一个实用的生活小技巧:一个快速可视化二进制文件的方法。
$ (echo "P5 1024 16384 255"; cat wlOUASom2fI.img) > ./wlOUASom2fI.pgm
其中 1024 是宽度,16384 是高度(单位都是像素)。技巧来源于 https://blahcat.github.io/2018/12/02/quick-visualization-of-a-binary-file/。得到的 pgm 文件可以被许多图片查看器打开,效果如图:

这里,顶部的黑块高 128 个像素 (= 128 KB),这表明块大小必然小于等于 128 KB,否则第一块不可能会在 128 KB 之后出现其他的数据(因为只有一个分区,其他的分区表项都是空的)。因为块大小是 2 的次幂 KB,所以 1 MB 的块必然在第一块盘上(对应的位置是 1 MB / 8 = 131072 B = 0x20000)。
让我们来看看吧!
*
00020010 00 00 58 46 53 42 00 00 10 00 00 00 00 00 00 00 |..XFSB..........|
00020020 7e fb 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |~...............|
XFSB 是 XFS 文件系统超级块 (superblock) 的特征。说明第一个分区是 XFS 文件系统。除此之外,我们还可以知道最后一块盘是哪个——因为 GPT 会在磁盘的末尾放上备用分区表。
$ for i in *.img; do echo $i && hexdump -C $i | grep 'EFI PART'; done
1GHGGrmaMM0.img
5qiSQnlrA4Y.img
ID7sM2RWkyI.img
00fffe00 45 46 49 20 50 41 52 54 00 00 01 00 5c 00 00 00 |EFI PART....\...|
RApjvIxRlu0.img
d3Be7V0EVKo.img
eRL2MQSdOjo.img
jCC60mutgoE.img
wlOUASom2fI.img
00000200 45 46 49 20 50 41 52 54 00 00 01 00 5c 00 00 00 |EFI PART....\...|
证明了 ID7sM2RWkyI.img 是最后一块盘。
接下来问题的焦点是:块大小到底是多少?我们来看看可能的块边缘(0x10000 = 64 KB 的倍数)的情况吧。
$ for i in *.img; do echo $i && hexdump -C $i | grep '0000 '; done > ./tmp1
会发现一些有意义的字符串:
d3Be7V0EVKo.img
...
008c0000 69 76 65 6e 65 73 73 5f 75 6e 64 65 72 5f 6c 6f |iveness_under_lo|
008d0000 74 20 2f 53 75 62 74 79 70 65 20 2f 4c 69 6e 6b |t /Subtype /Link|
使用十六进制编辑器定位到这里,可以明显发现:
- 0x8c0000 前面的数据被截断了,代表 0x8c0000 是块大小的倍数;
- 0x8c0000 到 0x8dd906 是明显连续的数据,中间没有被截断;
- 0x8e0000 处出现了明显的截断。
所以可以推得块大小是 0x8e0000 - 0x8c0000 = 131072 B = 128 KB。
最后一步我们需要知道盘的顺序。虽然可以找刚好被截断的文件一个个推顺序,但是玩拼图不是更简单吗?让我们来点数据科学,用炼丹的同学最喜欢的 matplotlib 试试(
import numpy as np
import matplotlib.pyplot as plt
files = ['wlOUASom2fI.img', '1GHGGrmaMM0.img', '5qiSQnlrA4Y.img',
'RApjvIxRlu0.img', 'd3Be7V0EVKo.img', 'eRL2MQSdOjo.img',
'jCC60mutgoE.img', 'ID7sM2RWkyI.img'] # 第一块和最后一块盘是已知的
start = 0 # 从头开始读取
sz = 16 * 1024 * 1024 # 读取的文件大小 (bytes)
n = 128 * 1024 # 块大小
b = 1024 # 用于求和的小块大小
data = []
for fn in files:
with open("./" + fn, 'rb') as f:
f.seek(start, 0)
data.append(np.frombuffer(f.read(sz), dtype=np.uint8))
p = [[np.sum(data[f][i * n + j * b : i * n + j * b + b]) for f in range(len(files)) for j in range(n // b)] for i in range(sz // n)] # i: 块, j: 小块, f: 文件
graph = np.array(p)
print(graph.shape)
plt.matshow(graph, aspect='auto')
plt.xticks(np.arange(0, 1024.1, step=128))
plt.yticks(np.arange(0, 128.1, step=16))
plt.show()
可视化的思路是:将数据按照顺序和块大小拼起来,每 b (1024) 字节(小块)的数据求和得到的结果作为得到的矩阵 p 的一项。图中横轴对应不同的盘(每 128 对应不同的盘),竖轴对应盘的不同位置。如果拼图拼得不对,预期的结果是出现裂痕:
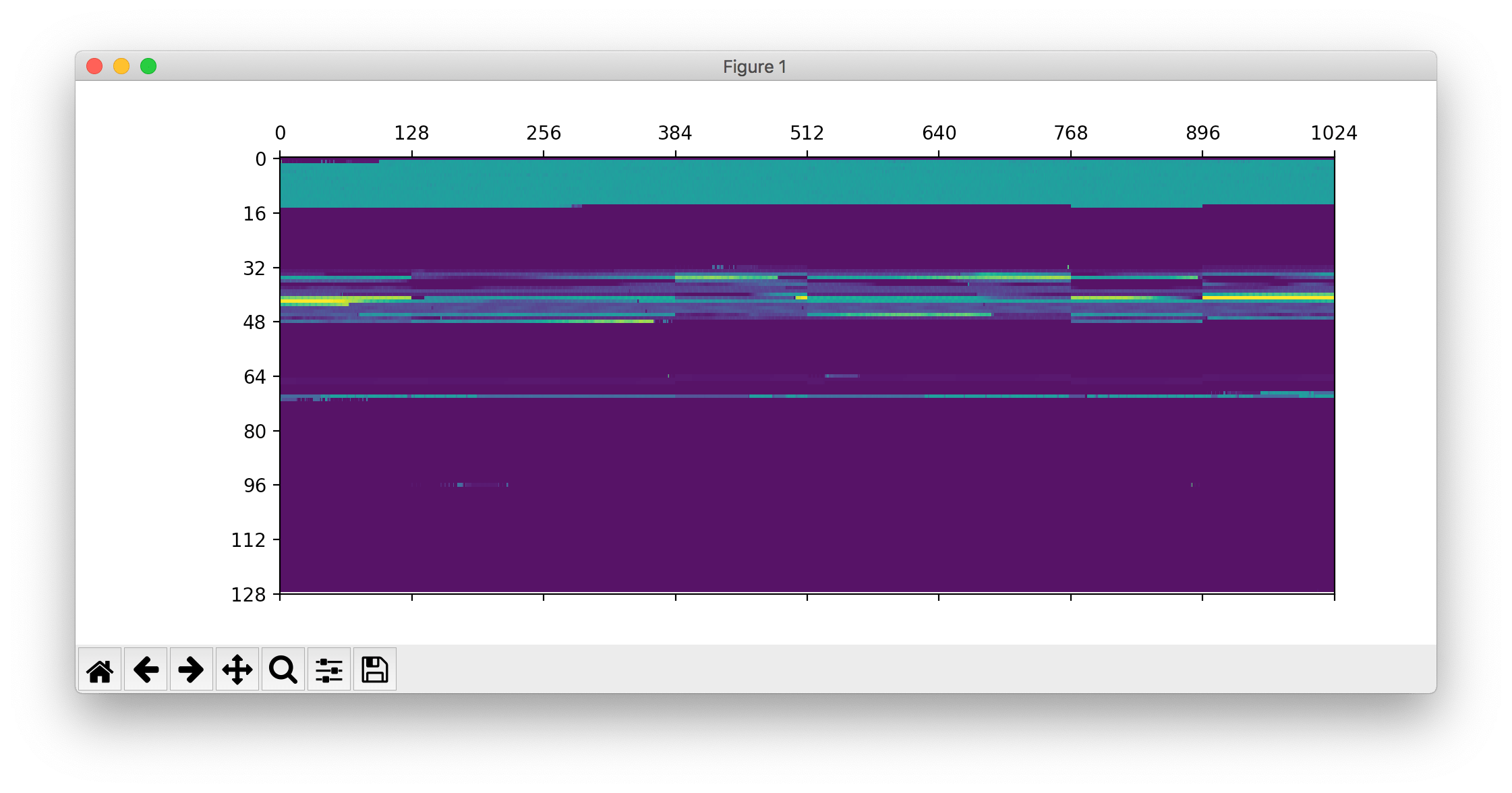
相信各位同学都会玩拼图,怎么拼这里就不详细阐述了,最后得到的正确顺序是:
files = ['wlOUASom2fI.img', 'jCC60mutgoE.img', '1GHGGrmaMM0.img',
'5qiSQnlrA4Y.img', 'd3Be7V0EVKo.img', 'eRL2MQSdOjo.img',
'RApjvIxRlu0.img', 'ID7sM2RWkyI.img']
拼出来:

最后一个问题:怎么挂载分区?
写脚本拼成一个大文件是可以的,但是在现实中,阵列的大小会上至少几 TB 的情况下这么搞是不现实的。这种需求可以用 mdadm --build(用于拼接无 RAID superblock 的阵列)解决:
$ sudo losetup --read-only /dev/loop0 wlOUASom2fI.img
$ sudo losetup --read-only /dev/loop1 jCC60mutgoE.img
$ sudo losetup --read-only /dev/loop2 1GHGGrmaMM0.img
$ sudo losetup --read-only /dev/loop3 5qiSQnlrA4Y.img
$ sudo losetup --read-only /dev/loop4 d3Be7V0EVKo.img
$ sudo losetup --read-only /dev/loop5 eRL2MQSdOjo.img
$ sudo losetup --read-only /dev/loop6 RApjvIxRlu0.img
$ sudo losetup --read-only /dev/loop7 ID7sM2RWkyI.img
$ sudo mdadm --build --assume-clean --chunk=128 --level=0 --raid-devices=8 /dev/md0 /dev/loop{0..7}
mdadm: array /dev/md0 built and started.
别忘了 losetup 加上 --read-only,不然可能会有错误的写入。
第一个分区在 /dev/md0p1。
在实际操作中最后一个坑是 XFS 的只读挂载。XFS 即使挂载时设置了 -o ro,它也还是会在挂载时尝试恢复日志(这个过程需要写入),于是需要加 norecovery 参数。但是这里盘是 clean 的,所以不会触发这个坑点。
$ mkdir mountpoint
$ sudo mount -o ro /dev/md0p1 mountpoint/
$ cd mountpoint
$ python3 getflag.py
(输出省略)
Flag: flag{4857cdeac07d8456fcaedb61d07b0b7d}
RAID 0 小题结束。别忘了结束之后收拾残局(umount, mdadm --stop /dev/md0, losetup -D)
这道题的很多参数都是从三月份那次阵列恢复中实际拿的:包括盘的数量(我们的配置是 16 块盘的 RAID 10,它的一侧就是 8 块盘的 RAID 0)、块大小 (128 KB) 以及文件系统 (XFS)。
当然,暴力穷举也不是不行,可能性一共有 8! * 6 = 241920 种(块大小只考虑开头说的情况)。
RAID 5
本来没有这一小题,是后面加上的。RAID 5 还是有点稍微不一样的地方的。
以五块盘的 RAID 5 阵列为例子,很多教科书的介绍里都是这么排布的:
| 盘 1 | 盘 2 | 盘 3 | 盘 4 | 盘 5 |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | P |
| 4 | 5 | 6 | P | 7 |
| 8 | 9 | P | 10 | 11 |
| 12 | P | 13 | 14 | 15 |
| P | 16 | 17 | 18 | 19 |
(其中 P 是 parity,奇偶校验位,取相同行其他磁盘的块异或得到)
但是这不是唯一可能的排布方式。以上的排布称为 left-asymmetric。除此之外,还有 left-symmetric, right-asymmetric, right-symmetric 三种可能。
left-symmetric:
| 盘 1 | 盘 2 | 盘 3 | 盘 4 | 盘 5 |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | P |
| 5 | 6 | 7 | P | 4 |
| 10 | 11 | P | 8 | 9 |
| 15 | P | 12 | 13 | 14 |
| P | 16 | 17 | 18 | 19 |
right-asymmetric:
| 盘 1 | 盘 2 | 盘 3 | 盘 4 | 盘 5 |
|---|---|---|---|---|
| P | 0 | 1 | 2 | 3 |
| 4 | P | 5 | 6 | 7 |
| 8 | 9 | P | 10 | 11 |
| 12 | 13 | 14 | P | 15 |
| 16 | 17 | 18 | 19 | P |
right-symmetric:
| 盘 1 | 盘 2 | 盘 3 | 盘 4 | 盘 5 |
|---|---|---|---|---|
| P | 0 | 1 | 2 | 3 |
| 7 | P | 4 | 5 | 6 |
| 10 | 11 | P | 8 | 9 |
| 13 | 14 | 15 | P | 12 |
| 16 | 17 | 18 | 19 | P |
RAID 5 的主要难点就是要知道以上排布的方法。(可能我构造的时候应该搞个 right-symmetric 的……这样难度可能能和分值更匹配)
按照惯例,file:
$ file *
3D8qN9DH91Q.img: data
3RlmViivyG8.img: DOS/MBR boot sector; partition 1 : ID=0xee, start-CHS (0x0,0,2), end-CHS (0x3ff,255,63), startsector 1, 262143 sectors, extended partition table (last)
60kE0MQisyY.img: DOS/MBR boot sector; partition 1 : ID=0xee, start-CHS (0x0,0,2), end-CHS (0x3ff,255,63), startsector 1, 262143 sectors, extended partition table (last)
IrYp6co7Gos.img: data
QjTgmgmwXAM.img: data
两块盘有 GPT 分区表。这表明 3RlmViivyG8.img 和 60kE0MQisyY.img 其中有一个是第一块盘,有一个是最后一块盘(parity)。用上面 RAID 0 分析的方法就会发现,两道题的分区表信息是几乎一样的(做的时候摸了)。
我自己做的时候得到块大小的方法可能比较 tricky:将所有盘都用上面的生活小技巧可视化看一下,可以发现有很多高为 64 像素的块,并且找不到高为 32 像素的块,表明块大小很可能就是 64 KB。
如果排布是 left 的,那么第一个 parity 块在最后一个磁盘上,第一个分区的 superblock (1 MB 的位置) 就在第二块盘的 256 KB (= 0x40000) 的位置上(像上面一样画表格,可以看到在表格的第五行)。把所有盘看一遍,可以看到 3RlmViivyG8.img 和 IrYp6co7Gos.img:
00040430 91 3d 71 61 01 00 ff ff 53 ef 01 00 01 00 00 00 |.=qa....S.......|
00040480 00 00 00 00 00 00 00 00 2f 68 6f 6d 65 2f 64 65 |......../home/de|
00040490 62 69 61 6e 2f 68 61 63 6b 65 72 67 61 6d 65 2f |bian/hackergame/|
位于 0x40430 的 53 ef 是 ext 文件系统超级块的 signature。说明这是个 ext 文件系统(ext2/3/4)。因为 3RlmViivyG8.img 不可能是第二块盘,所以只有可能是 IrYp6co7Gos.img 为第二块盘。同时得到 3RlmViivyG8.img 是第一块盘,60kE0MQisyY.img 是最后一块盘。
如果排布是 right 的,那么第一个分区的 superblock 还会在第一块盘上(parity 此时在最后一块盘上)。但是 IrYp6co7Gos.img 和 3RlmViivyG8.img 有 ext4 signature,代表它们分别为第一块盘和最后一块盘,和解析 GPT 数据得到的结论矛盾。
如何给盘排序呢?还是拼图吧。画出来就能发现 parity 是相当有特征的。
import numpy as np
import matplotlib.pyplot as plt
files = ["3RlmViivyG8.img",
"IrYp6co7Gos.img",
"QjTgmgmwXAM.img",
"3D8qN9DH91Q.img",
"60kE0MQisyY.img",] # 第 1、2、5 块盘是已知的
start = 3 * 1024 * 1024 # 后面的特征稍微明显一点
sz = 1 * 1024 * 1024 # 读取的文件大小 (bytes)
n = 1 * 1024 # 这里不是块大小,小一点的话特征更明显
b = 256 # 用于求和的小块大小
data = []
for fn in files:
with open("./" + fn, 'rb') as f:
f.seek(start, 0)
data.append(np.frombuffer(f.read(sz), dtype=np.uint8))
p = [[np.sum(data[f][i * n + j * b : i * n + j * b + b]) for f in range(len(files)) for j in range(n // b)] for i in range(sz // n)] # i: 块, j: 小块, f: 文件
graph = np.array(p)
print(graph.shape)
plt.matshow(graph, aspect='auto')
plt.show()
得到图如下:
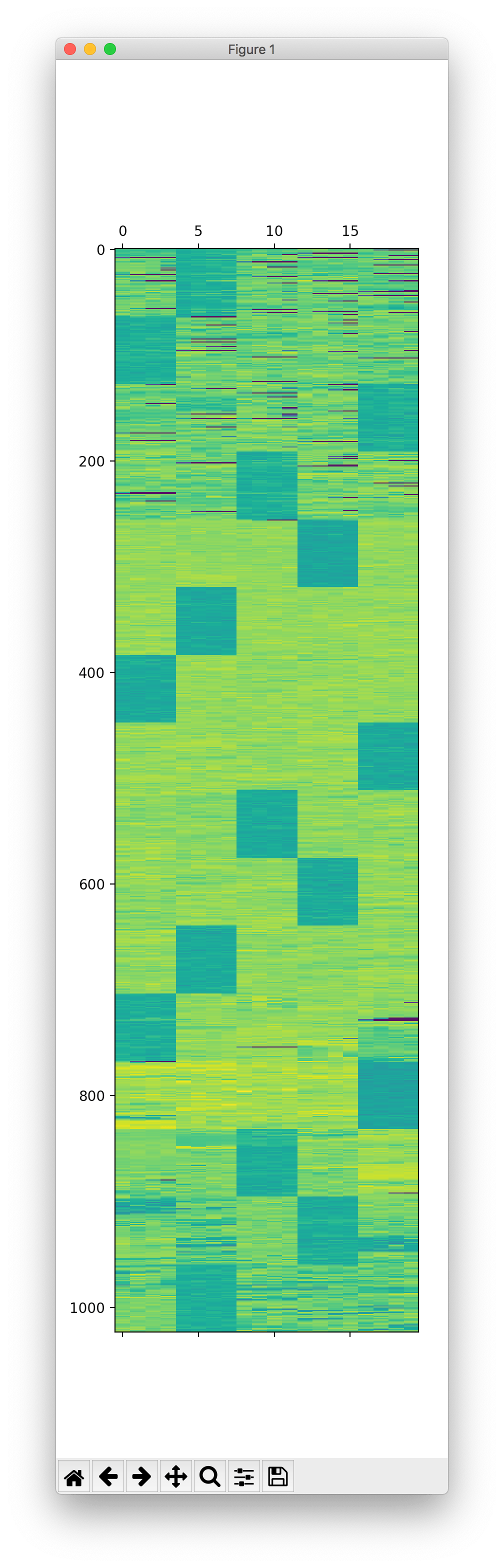
很明显,第三四块盘要换个顺序,最后正确的图:
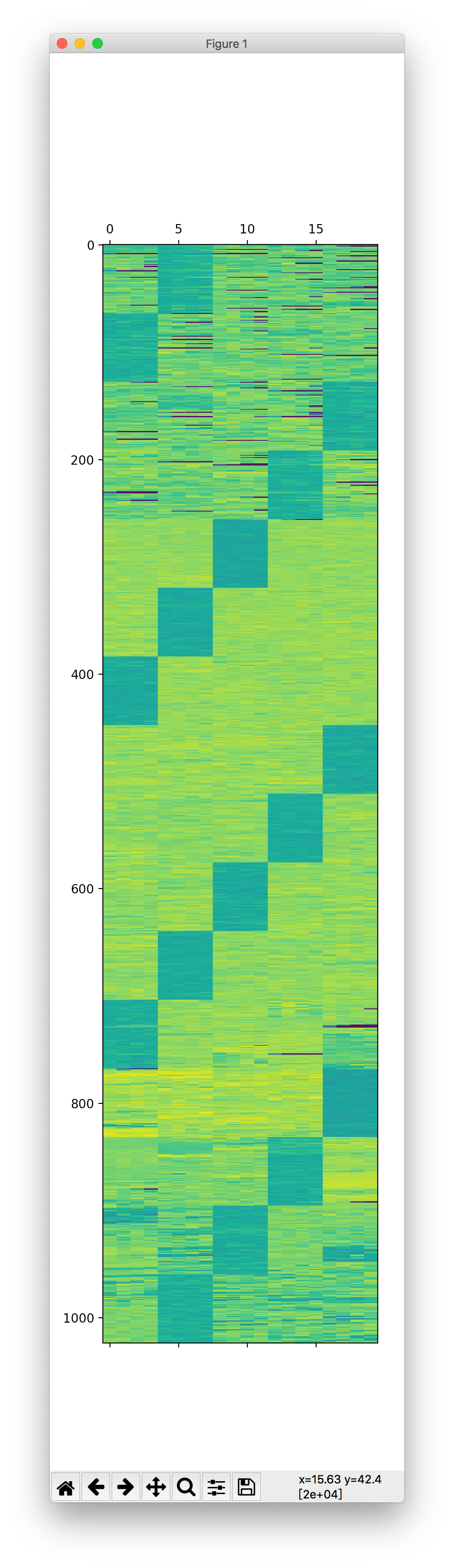
顺序:
files = ["3RlmViivyG8.img",
"IrYp6co7Gos.img",
"3D8qN9DH91Q.img",
"QjTgmgmwXAM.img",
"60kE0MQisyY.img",]
因为 mdadm --build 不支持 RAID5,所以当然还是可以试试写脚本自己拼,或者想办法让 mdadm 来 assemble(会覆盖掉每块盘开头一部分),不过有个更有意思的做法:写个 fuse 小脚本(这也是 @zzh1996 当时确认文件能恢复的方法)
#!/usr/bin/env python3
# pip3 install fusepy
import logging
import sys
import os
import time
from errno import ENOENT
from threading import Lock
from stat import S_IFDIR, S_IFLNK, S_IFREG
from fuse import FUSE, FuseOSError, Operations, LoggingMixIn
class MyFS(LoggingMixIn, Operations):
def __init__(self):
self.rwlock = Lock()
self.blocksize = 64 * 1024
self.disk_num = 5
self.imgs = [open('./disk' + str(i) + ".img", 'rb') for i in range(1, self.disk_num + 1)]
self.size = 0
self.offset = 0 # set offset when image is created by mdadm (0x100000)
for i in range(1, self.disk_num):
self.size += os.path.getsize('./disk' + str(i) + ".img") - self.offset
def getattr(self, path, fh=None):
if path == '/img':
st_mtime = 0
st_atime = 0
st_ctime = 0
st_uid = 0
st_gid = 0
st_mode = S_IFREG | 0o444
st_size = self.size
st_nlink = 1
return dict(st_mtime=st_mtime, st_atime=st_atime, st_ctime=st_ctime, st_uid=st_uid,
st_gid=st_gid, st_mode=st_mode, st_size=st_size, st_nlink=st_nlink)
elif path == '/':
st_mtime = 0
st_atime = 0
st_ctime = 0
st_uid = 0
st_gid = 0
st_mode = S_IFDIR | 0o755
st_size = 0
st_nlink = 1
return dict(st_mtime=st_mtime, st_atime=st_atime, st_ctime=st_ctime, st_uid=st_uid,
st_gid=st_gid, st_mode=st_mode, st_size=st_size, st_nlink=st_nlink)
else:
raise FuseOSError(ENOENT)
def read(self, path, size, offset, fh=None):
path = path[1:]
if path == 'img':
with self.rwlock:
start = offset
end = offset + size
block_start = start // self.blocksize
block_end = (end - 1) // self.blocksize
data = b''
for b in range(block_start, block_end + 1):
block_disk = b % (self.disk_num - 1)
parity = self.disk_num - 1 - (b // (self.disk_num - 1)) % self.disk_num
# left-asymmetric
# if block_disk >= parity:
# block_disk += 1
# left-symmetric
block_disk = (parity + block_disk + 1) % self.disk_num
assert block_disk == b % self.disk_num
f = self.imgs[block_disk]
f.seek(b // (self.disk_num - 1) * self.blocksize + self.offset, 0)
data += f.read(self.blocksize)
return data[start % self.blocksize : start % self.blocksize + size]
else:
raise FuseOSError(ENOENT)
def readdir(self, path, fh=None):
items = ['.', '..', 'img']
path = path[1:]
if path == '':
return items
else:
raise FuseOSError(ENOENT)
if __name__ == '__main__':
logging.basicConfig(level=logging.INFO)
fuse = FUSE(MyFS(), sys.argv[1], foreground=True, allow_other=True)
$ ln -s ./3RlmViivyG8.img disk1.img
$ ln -s ./IrYp6co7Gos.img disk2.img
$ ln -s ./3D8qN9DH91Q.img disk3.img
$ ln -s ./QjTgmgmwXAM.img disk4.img
$ ln -s ./60kE0MQisyY.img disk5.img
$ mkdir tmp
$ python3 -m venv venv
$ . venv/bin/activate
(venv) $ pip3 install fusepy
(venv) $ python3 fusemount.py tmp
然后开个新 terminal:
$ mkdir mountpoint
$ cd tmp
$ sudo mount -o ro,offset=$((1024*1024)),loop ./img ../mountpoint/
$ cd ../mountpoint/
$ python3 getflag.py
(输出省略)
Flag: flag{a18325a1ec0f58292908455c2df8ffcd}
就好了。最后发现排布是 left-symmetric。Left-symmetric 也是 mdadm 创建 RAID 5 阵列的默认值,因为它在连续读取大文件时相比于 left-asymmetric 有更好的性能(例如,连续读取 0-4 号块的时候,读取可以被均匀分布到每一块盘上)。同时也可以发现,如果 RAID 5 坏了一块盘,虽然阵列还能用,但是有性能损失(因为要读取所有其他的硬盘,并且进行异或计算之后才能够确认损坏硬盘那里对应的值)。
(一个无关的备注:不建议将 RAID 5 用于大硬盘阵列,否则在重建时第二块硬盘发生错误导致重建失败的可能性相当高。)
附录
RAID 0 盘的文件内容:
- 大物显微镜实验拍的照片。为了减少 RAID 0 的难度(避免出现大量高度压缩的文件导致拼图困难),转换成了 BMP 格式,部分色彩有丢失;
- 随便打印的的几个 PDF;
- 自己写的没有对外公开的一些代码;
- 2020 年科大 OSH 实验 1 第三个测试程序 在自己写 PoC 时候的录屏。因为太二次……那啥了,最后出实验换了一张图就是了。程序代码,图片需要自己导出 XPM 格式后
#include。
RAID 5 盘的文件内容:
- GRUB 的源代码,删掉了一些东西,同时改了一个 C 文件。相关的故事
- 调研 parcel 游戏引擎时用开源的代码糊出来东西,本来是准备改改用来做隔壁赛博餐厅的,但是后来自己忙 + 餐厅的出题人发现可以直接用前端栈解决,就没有用这个方案。
查过论文的同学可能知道有篇论文讲了阵列恢复的主题:Generic RAID reassembly using block-level entropy。但是,非常不幸,他们开源的代码,对这两道题不工作。我尝试编译并且修了类型的问题,结果 RAID 0 只能识别出正确的块大小,给的顺序是错误的;RAID 5 根本没法用。
